Mixtures of Experts as an Auction: The BASE Transformer
How re-formulating MoE as an auction guarantees perfect load balance without auxiliary losses - and beats the Switch Transformer
Sparse Mixtures of Experts (MoE) has become a key technology in the latest generation of LLMs such as Google’s Switch Transformer, OpenAI’s GPT-4, Mistral AI’s Mixtral-8x7b, and more. In a nutshell, sparse MoE is an extremely powerful technology because - in theory - it allows us to scale up capacity of any model with a computational complexity of O(1)!
However, as is often the case, the devil lies in the details, and getting sparse MoE to work correctly requires to get these details exactly right.
Last week, we learned about the Switch Transformer, which demonstrated for the first time the remarkable scaling properties that can be achieved when replacing the FFN layers in a Transformer model with sparse MoEs, achieving 7x speed-up over a standard, dense, Transformer.
As it turns out, the greedy routing strategy in the Switch Transformer isn’t the only way (and perhaps not the best way) to assign tokens to experts. This week, we’ll learn about the BASE (“Balanced Assignment of Experts”, Lewis et al 2021) algorithm, which - like Switch - is used to build sparse Transformer models, but - unlike Switch -uses a non-greedy auction algorithm to optimally assign tokens to experts. We’ll learn about
the balanced assignment problem: why token-expert balance matters, and how it’s been solved before,
BASE’s auction algorithm: how it works and how it’s incorporated into the Transformer architecture,
BASE inference: why we use standard, greedy, routing at inference time and how this changes token-expert balance, and
empirical results with BASE: how the BASE Transformer stacks up against the Switch Transformer.
Let’s get started.
The balanced token assignment problem
In MoE, we model a prediction y as a weighted sum of experts E, where the weights are determined by a gate G. In ordinary, dense MoE, we run each expert over each tokens in each training example, and then compute the weighted sum over all expert outputs. This approach works, but it is computationally expensive - the complexity is O(E).
In sparse MoE, we instead send every token to just a single expert, namely the expert with the highest gate value, to save cost. Theoretically, this should allow us to increase modeling capacity with O(1) computational complexity - we just need extra memory to store the additional experts.
The balanced token assignment problem is the problem of making sure that each expert receives a roughly equal number of tokens. If tokens assignments are imbalanced, e.g. a single expert receives most of the tokens, this introduces computational bottlenecks. Ideally, each expert should receive an equal number of tokens in each training iteration. This problem led to the invention of auxiliary losses such as expert diversity loss, which is minimized if all experts are being utilized equally.
In contrast, the key idea in BASE is to guarantee perfectly balanced token assignment without the need for any additional knobs such as auxiliary losses. This works by re-formulating the sparse MoE algorithm as an auction.
BASE’s auction algorithm

The key idea in BASE is to formulate MoE as an auction, where the bidders are the tokens, and the bids are being placed on the experts. Just like in any auction, this scheme ensures that each expert is being assigned to the token (bidder) for which it is the most useful!
BASEs’s auction algorithm is borrowed from Bertsekas 1992, making it (coincidentally) roughly as old as the MoE algorithm itself! Here’s how the algorithm works:
Bidding Process: Each token acts like a bidder in an auction. The token "bids" for the expert it prefers the most, based on its affinity with that expert, which is determined by the gating function. The bid indicates how well a token benefits from a particular expert.
Assignment and Prices: Each expert has a "price" that changes dynamically. When a token bids for an expert, it bids an amount equal to the current price of that expert plus a small increment. The expert is tentatively assigned to the token that bids the highest amount. As a result of this bidding, the price of the expert increases, reflecting its demand.
Iterative Process: This process is iterative. Tokens that are outbid will have to bid again, possibly for a different expert. This means tokens repeatedly evaluate their affinity towards different experts, adjusting their bids based on the changing prices of the experts.
Convergence: The process continues until all tokens are assigned to experts, and there are no more bids that can change the assignment. At this point, the algorithm has found an optimal or near-optimal assignment of tokens to experts.
Let’s consider a simplified example with the 2 tokens “dog” and “cat”, 3 experts, and the following gate values:
G("dog") = [0.3, 0.6, 0.1]
G("cat") = [0.2, 0.7, 0.1]
Standard hard routing would simply route both embeddings for “dog” and “cat” to expert #2, because this is the expert with the largest gate value, i.e. the most suitable expert. The result in BASE on the other hand would be different: we’d route “cat” to expert #2, and “dog” to expert #1. This is because “cat” made a higher bid for the second expert than “dog”, and “dog” consequently had to select its second choice instead.
From BASE layers to BASE Transformer
BASE can be thought of as a layer that translates input sequences to output sequences, where each token in the input sequence is being processed by a distinct expert. We can weave it into the Transformer model by replacing the FFN layers (blue boxes) in the Transformer with BASE layers:
One design consideration is how many of the total Transformer blocks we should replace with BASE Transformer blocks - the authors consider 1, 3, and 5, and find the best performance with 3 (they call this model “BASE x 3”).
Empirical results: beating the Switch Transformer
The authors compare against two competing sparse MoE algorithms:
the top-k MoE algorithm introduced in Shazeer et al 2017, with a load balancing loss parameter of 0.01 (which I wrote about here), and
the Switch Transformer introduced in Fedus et al 2022, with a capacity factor of 1.0 (which I wrote about here).
All experiments were run on 128 32GB V100 GPUs, with one expert per GPU per MoE layer. All models were trained on the 100B-token RoBERTa corpus.
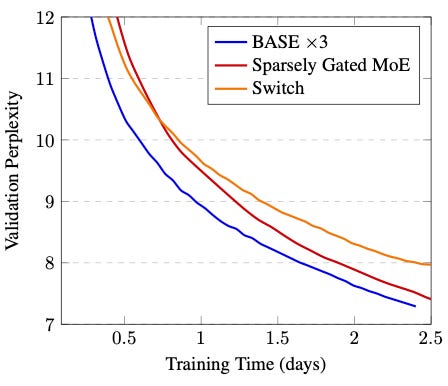
The result? “BASE x 3”, that is, the Transformer model with 3 BASE blocks, performs at least on par with the Switch Transformer and top-k MoE, as shown in the following plot:
In addition, BASE is fast: the authors find 16% higher throughput (tokens/s) compared to Switch Transformer. In other words, if we train a Switch Transformer for 7 days, the BASE Transformer would have the same performance in just 6 days. BASE is more efficient because it guarantees perfect load balancing during training, which is not guaranteed in the Switch Transformer.
Inference with BASE
Interestingly, BASE behaves differently at inference time compared to training time: at inference time, we simply (greedily) route tokens to the best expert as if it were a standard sparse MoE model. There are two reasons for this.
First, at inference time the most important objective we care about is modeling accuracy, given a fixed latency budget. A little bit of load imbalance is ok, as long as we can still serve the model within that budget. This is different from training, where a small imbalance can have a large impact on throughput and hence training speed.
Second, in theory BASE’s training scheme should already balance token-to-expert assignments, so that we don’t actually need the auction algorithm any more at inference time. Indeed, this appears to be (almost) the case, as we see in the figure below.
This figure shows the percentage of all tokens routed to each expert, as a function of expert, sorted by the expert’s overall usage decreasingly from left to right. At training time (light blue curve), all experts are being used equally, thanks to the auction algorithm. At inference time (dark blue curve), the assignment is more imbalanced because BASE is replaced with a simple greedy assignment, but still within 4%. The resulting imbalance is however worse than the Switch Transformer (green curve) or top-k routing (red curve), for which we see a maximum imbalance of no more than 2%.
BASE, in summary, guarantees perfect load balance only at training time - at inference time, it is actually more imbalanced than the Switch Transformer!
Expert specialization in BASE
It is also interesting to investigate what exactly expert specialize in. In order to do that, the authors examine the top 5 tokens per expert over the entire training set, that is, the most frequent tokens routed to that expert. Here’s the result for a few example experts:
Intuitively, the results make sense: we see word clusters corresponding to quantities (5), numbers (42), possessives (125), work (62), finance (98), and so on. This again illustrates MoE’s “divide-and-conquer” behavior: the gate learns to segregate the data into clusters, and the experts specialize in their (randomly assigned) clusters.
Summary
To recap:
The balanced token assignment problem is the problem of making sure that each expert in sparse MoE is being assigned the same number of tokens in a batch of training data. This is important to prevent computational bottlenecks and therefore make training as efficient as possible.
BASE (balanced assignment of experts) solves this problem by replacing the standard, greedy, routing with an auction algorithm, where tokens bid on experts, and experts are assigned according to the highest bidder. The maximum bids are simply determined by the gate outputs.
BASE guarantees perfect balance at training time, however not at inference time, where we default to the standard greedy assignment such as to maximize predictive accuracy. Empirically, the imbalance is however no more than 4%.
BASE’s predictive accuracy is on par, if not slightly better, compared to the Switch Transformer or top-k routing, while at the same time achieving 16% better throughput in terms of tokens per second.
Taking a step back, BASE showed that one of the most important skills needed to advance the state of the art in ML is “thinking outside the box”: while previous work took routing as a given and tried to fix the balancing problem downstream with auxiliary losses, the authors of BASE thought from first principles and challenged the assumption of using greedy routing in the first place - with success!
Machine Learning Frontiers is a one-man startup with a mission to open the black box and make modern ML algorithms accessible to anyone. If you’d like to show your support for this mission, consider becoming a paid subscriber. Paid subscribers also get access to the growing research archive.