Understanding Embedding Dimensional Collapse in Recommender Systems
Why standard ranking models fail to scale - and how to fix it
While embedding dimensional collapse has been observed in self-supervised learning at least since 2021 (Hua et al 2021), it has only recently raised attention in recommender systems, or more specifically, the problem of scaling up recommender systems by increasing parameter count.
A good way to picture this phenomenon is to imagine a 3-dimensional space, where the embedding vectors all lie on a 2-dimensional plane: this would be a 2D “collapse” within a 3D space. Note that this type of collapse is different from “embedding collapse”, which refers to the phenomenon of all embedding vectors collapsing into a single point. In other words, embedding collapse is a special case of embedding dimensional collapse where the subspace spanned by the embedding vectors is just a single point (0D).

Luckily, the recent paper “On the Embedding Collapse When Scaling Up Recommendation Models” (Guo et al 2024) sheds some interesting insights. Let’s take a look.
The “standard model” of recommender systems
As a brief reminder, a typical ranking model in a recommender systems usually consists of 3 stages, the embedding layer, feature interactions, and the prediction layer, which we may mathematically summarize as the following 3 equations,
where
e_i is the embedding vector corresponding to feature i (out of N), generated using the embedding lookup table E_i,
“I” is the interaction module which computes all possible interactions between the input features, for example using dot products or element-wise products. Different interaction modules have emerged over the recent years, with Deep and Cross (DCN) being one of the most successful ones.
F(h) processes the output from the interaction module and computes a prediction logit. F can be as simple as an MLP, but for multi-task problems in particular (e.g. one task per conversion in the recommender system), multi-gated mixtures of experts (MMoE) have been found to work particularly well.
This 3-equation recipe has become a widely adopted paradigm for recommender systems; in Physics terminology, a “standard model”, if you will.
Failure to scale
Which brings us to the main problem of this standard model, it does not “scale”, meaning, increasing the total number of model parameters and hence the model’s capacity does not make the model predict better. This contradicts one of the most basic intuitions in Machine Learning, namely that more parameters make better predictions.
But don’t just take my word, believe the data. Here’s a good plot illustrating this failure to scale. As we scale up the model’s parameter count from 1x to 10x (x-axis), the relative test AUC on the Criteo display ads dataset does not improve (y-axis), no matter which interaction module we use in the model. The different lines in the plot correspond to different choices of the interaction module I in the model, DCNv2 being the best one.
Proving embedding dimensional collapse
In order to prove that this failure to scale is indeed caused by embedding dimensional collapse, a useful diagnostic tool is singular value decomposition (SVD): we decompose a feature’s embedding matrix (where the columns correspond to the different embedding dimensions and the rows correspond to the training examples) as
where Σ is a diagonal matrix, where the values on the diagonal are the singular values of matrix E. Most important for our problem, if some of the singular values are vanishing, this means that E does not fully utilize all dimensions - it has “collapsed”.
And indeed, this is what we measure. The chart below shows the singular values for the embedding tables across features (y-axis), sorted by magnitude of the singular value (x-axis) in a DCNv2 model, where the color indicates the singular value, light red being 0.
Scaling up a DCNv2 model is apparently useless: even as we increase the embedding space, the model does not utilize that additional space — aka, embedding dimensional collapse.
The Interaction-Collapse Theory
Which brings us to the question of why embeddings dimensions in the standard model (a model consisting of embedding tables, learned feature interactions, and a final prediction layer) are collapsing.
Here, the authors introduce a hypothesis they call “interaction-collapse theory”. In the authors’ words,
In feature interaction of recommendation models, fields with low information-abundance embeddings constrain the information abundance of other fields, resulting in collapsed embedding matrices.
This needs unpacking. First, “information abundance” (IA) is a metric designed to measure how “collapsed” a feature is. Technically, it measures the sum of all singular values divided by the maximum singular value for an embedding table. Hence if the feature is collapsed, we have lots of zeros in the numerator and hence a small information abundance.
In other words, the existence of a single low-IA feature is sufficient to make all other features collapse into low-IA as well, just by interacting with it!
The intuition behind this claim is related to dominance in feature space interactions. When the two features interact, the low-IA feature may act as a bottleneck, limiting the expressiveness of the high-IA feature. This happens because the model prioritizes interactions with frequent or dominant patterns, causing more informative or rare patterns to lose significance. As a result, embeddings representing the high-IA feature collapse into a restricted space, reducing the model's ability to generalize effectively.
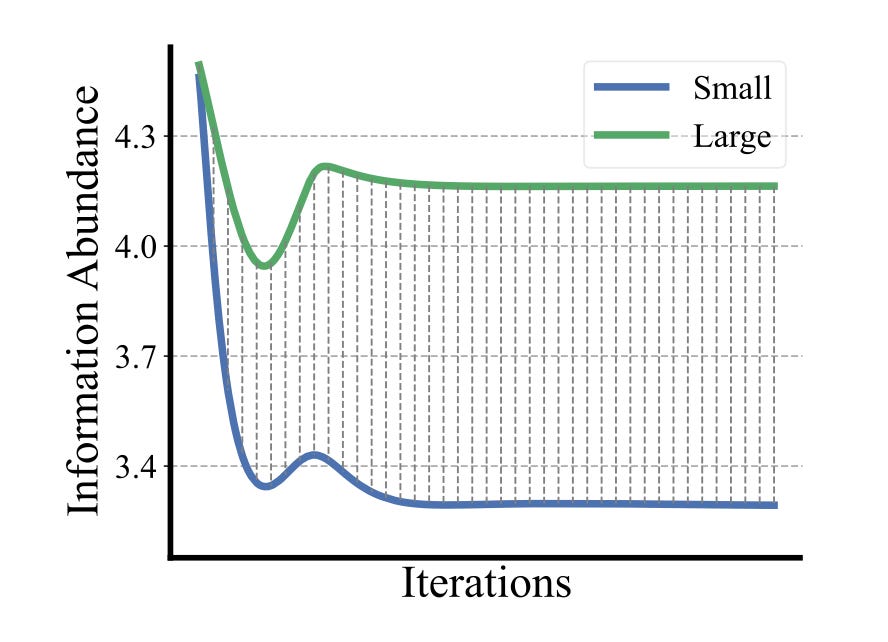
One way the authors prove this claim is by designing a toy experiment with 3 features, 2 of them with high IA, one of them with low IA, and then measure what happens to one of the high-IA feature’s IA over the course of model training as it interacts with either the other high-IA feature or the low-IA feature. Alas, in the latter case, we can indeed witness the collapse (see the blue curve in the plot below) — a smoking gun to prove interaction-collapse theory.
Fixing embedding dimensional collapse
In order to fix the collapse problem, the authors introduce the multi-embedding paradigm: instead of having just a single embedding table per feature, we have N of them, along with N interaction modules, one for each embedding table, as shown on the right side of the following illustration:
The hypothesis behind this approach is that all of these embedding tables will collapse differently, hence preserving overall more information compared to having just a single embedding table. And indeed, the authors show better scaling properties of multi-embedding models compared to their single-embedding counterparts. Here, for example, are the test AUC results on Criteo for xDeepFM and DCNv2, as a function of the scale-up factor:
It is interesting to see that even without multi-embeddings DCNv2 already scales much better than xDeepFM. The exact reasons for this discrepancy are not clear but I would suspect an important contributor to DCNv2’s favorable intrinsic scaling properties are its low-rank factorization algorithm as well as its information gating layers to reduce cross noise. (I covered these in detail in a previous issue.)
Ultimately, the authors show that switching from single-embedding to multi-embedding brings larger scale-up gains in an xDeepFM model (around 8bps) compared to a DCNv2 model (around 4bps).
Coda: is it worth it?
Is a 4bps Test AUC gain (assuming we use DCNv2) worth scaling up the model by 10x, hence resulting in 10x more memory required for training and serving the model?
The answer, at least for Tencent, appears to be a clear Yes. In the authors’ words:
After the online A/B testing in January 2023, the multi-embedding paradigm has been successfully deployed in Tencent’s Online Advertising Platform, one of the largest advertisement recommendation systems. Upgrading the click prediction model from the single-embedding paradigm to our proposed multi-embedding paradigm in WeChat Moments leads to a 3.9% GMV (Gross Merchandise Value) lift, which brings hundreds of millions of dollars in revenue lift per year.
Multi-embedding is an interesting new direction in recommender systems but it also feels rather “brute-force”. After all, as we know other domains such as contrastive learning or Mixture of Experts modeling, auxiliary losses are an alternative (and cheaper!) way to nudge a model to fully utilize the embedding space. It will be interesting to see if one could beat the multi-embedding paradigm with a few cleverly designed auxiliary loss functions instead.
Until next time!







