LoRA: Revolutionizing Large Language Model Adaptation without Fine-Tuning
Exploiting the low-rank nature of weight updates during fine-tuning results in orders of magnitude reduction in learnable parameters
Ever since the introduction of BERT in 2019, fine-tuning has been the standard approach to adapt large language models (LLMs) to downstream tasks. This changed with the introduction of LoRA (Hu et al 2021) which showed for the first time that the weight update matrix during fine-tuning can be drastically simplified using low-rank factorization, often with orders of magnitude fewer trainable parameters!
LoRA has become very popular in the NLP community because it allows us to adapt LLMs to downstream tasks faster, more robustly, and with smaller model footprints than ever before.
Let’s take a look at how it works.
The problem with fine-tuning
Google’s BERT (Devlin et al 2019) was a paradigm shift in NLP, in particular because of its introduction of the pre-training / fine-tuning paradigm: after unsupervised pre-training on a massive amount of text data, the model can be rapidly fine-tuned on a specific downstream task with relatively few labels because generic linguistic patterns have already been learnt. The success of BERT established the pre-training / fine-tuning paradigm as a standard practice in NLP.
Until LLMs became as massive as they are today. The BERT-Base model measured a modest (by today’s standards) 110 Million parameters in size, 3 orders of magnitude less than the 175 Billion-parameter GPT-3. This is a problem because for each downstream application we need to deploy a single, fine-tuned model artifact, each with the same size as the original, pre-trained model. This is a significant engineering challenge: for example, a 175B parameter model with 32-bit precision requires around 650GB of storage - for reference, even NVIDIA’s flagship H100 GPU has only 80GB of memory.
In the original BERT paper, the authors argued that fine-tuning is “straightforward” - this may have been the case with 2019’s model sizes, but perhaps not anymore with 2024’s.
Enter LoRA
Neural network weights are matrices. Consequently, the weight updates, the information about how much the weights change during model training, are matrices as well. For example, the weights in a neural network consisting of two fully connected layers with 1024 neurons each would form a 1024x1024-dimensional matrix, and so would their weight updates.
The key hypothesis behind LoRA is that the weight update matrices during fine-tuning of LLMs have low intrinsic rank.
This needs unpacking. A matrix with low intrinsic rank is a matrix that can be expressed using fewer parameters. For example, a 1024x1024 matrix with rank 10 can be expressed as the product of a 1024x10 matrix and a 10x1024 matrix, resulting in 3 orders of magnitude fewer parameters (2k vs 1M) - we call this low-rank factorization.
The lower a matrix’s intrinsic rank, the more redundant information it contains, and the more aggressively it can be compressed with low-rank factorization, with the lowest possible rank being 1, the matrix multiplication of two vectors.

In LoRA, instead of computing the entire weight update matrix ∆W given the pre-trained weights W, we approximate this matrix using low-rank factorization,
∆W = AB,where the shared dimension between A and B is the rank r, a free hyperparameter in the model. At serving time, all we need are the frozen pre-trained weights W as well as the (much smaller) matrices A and B to compute predictions y as:
y = Wx + ABxAdvantages of LoRA
LoRA introduces a plethora of advantages over fine-tuning, including:
Speed. Instead of having to learn all of the Billions of weights, we only need to learn the A and B matrices, which are typically orders of magnitudes smaller and hence faster to learn. Using GPT-3, the authors find that LoRA is 25% faster than fine-tuning.
Task-switching. In standard fine-tuning, we need a complete set of fine-tuned weights for each downstream task. When we have multiple tasks, this means that we have to swap very large model artifacts all the time. With LoRA, all we need are the pre-trained weights as well as one set of low-rank A/B matrices per task, allowing for instant switching.
Less overfitting. Because the number of parameters being learned in LoRA is usually orders of magnitude smaller than in fine-tuning, there’s less risk of overfitting.
Smaller model checkpoints. This can have practical advantages such as being able to log checkpoints more generously, which in turn allows for checkpoint averaging. For example, using rank 4, the footprint of GPT-3 is reduced by a factor of 10,000x, from 350GB to just 35MB!
Stability. LoRA results are remarkably stable, with different runs producing almost identical results. In contrast, fine-tuning has been shown to be so brittle that some practitioners recommend running many fine-tuning jobs with different seeds and picking the best one on a hold-out set, a practice that would be unacceptable to any serious scientists.
Which weights does LoRA adapt?
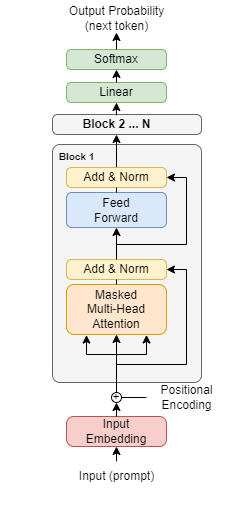
A Transformer block, the building block behind modern LLMs, contains multiple modules that LoRA could be applied to: the multi-head attention layers including the key, query, and value matrices, the Feed Forward MLP layers, the Add & Norm layers, the linear projection layer, or the Softmax layer. And those are just the weights - in addition we have all the corresponding biases as well.
Where should we add LoRA?
In the original LoRA paper, the authors only applied LoRA to the attention layers while freezing the rest of the model, both for “simplicity and parameter-efficiency”. While this approach may be among the most parameter-efficient (most of the weights are in the MLP layers, not the attention layers), it may not result in the best performance.
Indeed, on their github page, the authors explain that training the bias terms along with the LoRA matrices can be a parameter-efficient way to squeeze out extra performance. Sebastian Ruder showed that applying LoRA to all weights in a Transformer model instead of just the attention weights results in downstream accuracy improvements of 0.5-2%, depending on the task.
In short, while applying LoRA to just the attention weights and freezing everything else results in the most parameter savings, but applying it the entire model can result in better performance at the cost of more parameters.
How does LoRA perform?
The authors experimented with a suite LLMs: Roberta-Base, Roberta-Large, Deberta-XXL, GPT2-Medium, GPT2-Large, and — the largest of them all — GPT-3. In all cases, they replaced the attention layers with LoRA with rank r=8, and find consistently that performance matches or exceeds that of fine-tuning with orders of magnitude reduction in trainable parameters.
Among the most impressive results is the GPT-3 LoRA model, which reduces trainable parameters from 175B down to just 4.7M, a 5 orders of magnitude reduction, while even getting 2% better accuracy on MNLI-m, compared to fine-tuning.
Let that sink in: 2% better accuracy with 5 orders of magnitude fewer trainable parameters. This is a remarkable result, and it goes to show how surprisingly low-rank the weight update matrix really is.
How low-rank can we go?

Perhaps most surprisingly, LoRA works even with extremely small values of r such as 4, 2, or even 1, where we decompose the weight update matrix using just a single degree of freedom, similar to collaborative filtering. On the WikiSQL and MultNLI problem datasets, the authors found no statistically significant difference in performance when reducing the rank r=64 to r=1.
However, the lowest possible rank in LoRA will likely depend on the degree of difficulty of the downstream task relative to the pre-training task. For example, when adapting a language model in a different language than it was pre-trained on, we should expect that the weights need to change more drastically, requiring a much larger rank r.
In short, a reasonable rule of thumb could be this: the simpler the fine-tuning task, and the more closely related to the pre-training task, the lower rank we can get away with without performance degradations.
A new paradigm shift in NLP
LoRA enables us to adapt pre-trained LLMs to specific downstream tasks faster, more robustly, and with orders of magnitudes fewer learnable parameters compared to standard fine-tuning. This makes LoRA particularly useful for ML applications with very large LLMs that need to be fine-tuned for a number of different downstream tasks. Think e-commerce, where we need to classify product descriptions depending on a host of different regulations.
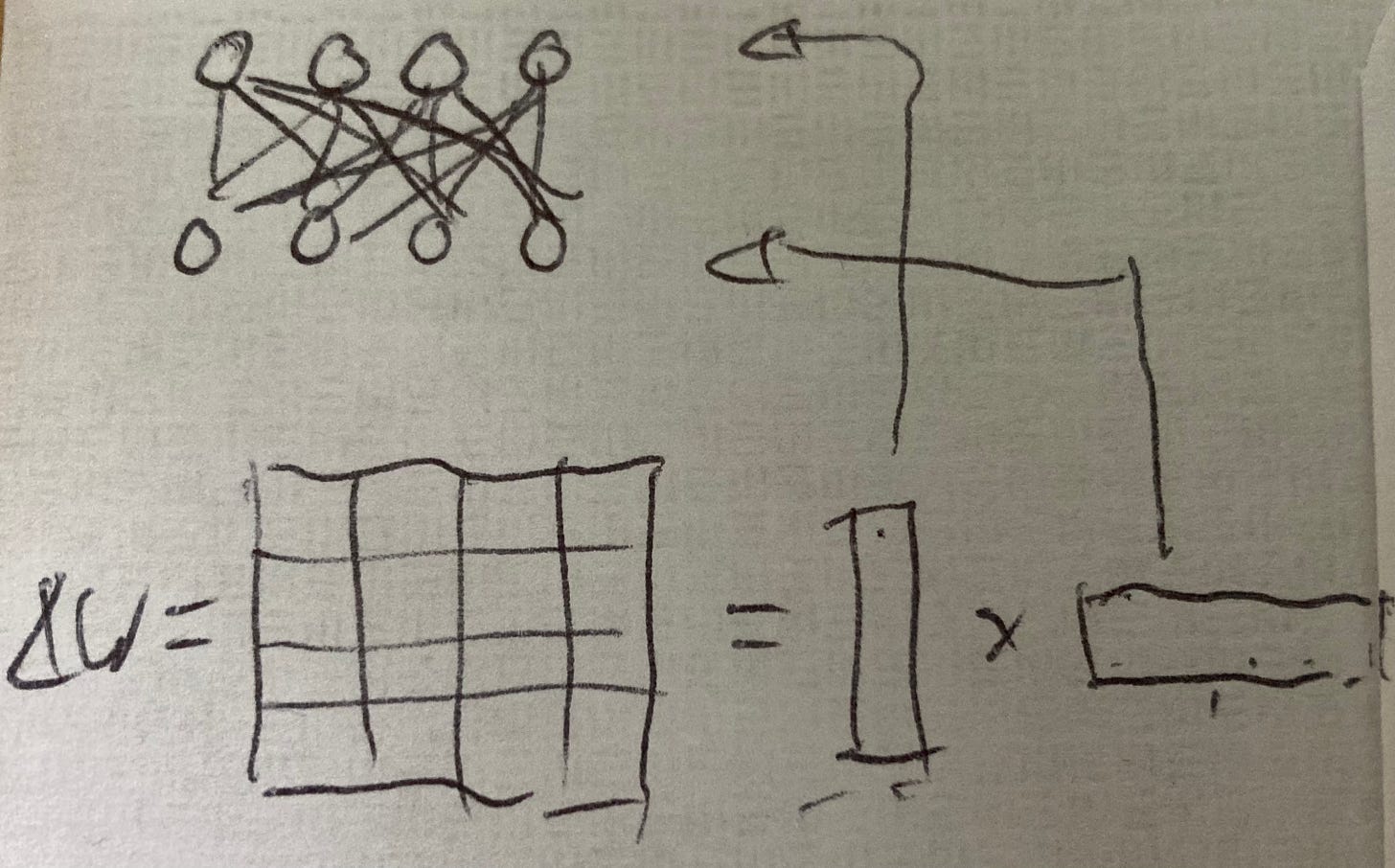
The success of LoRA proves that the weight updates during fine-tuning are surprisingly low-rank, in some cases as low as r=1. It is worth pausing for a moment the ask what exactly this result means. Consider a simplified case of 4 neurons fully connected to 4 neurons in the next layer, resulting in a 4x4 weight matrix. In the most extreme case, we could express the update to this matrix as the outer product of two 4-dimensional vectors that simply encode how much all weights attached to a particular neuron change:
This, then, is the key to understand the low-rank nature of fine-tuning: weights experience very coarse-grained and global updates, as opposed to local, fine-grained ones. In a very loose analogy, the model doesn’t really “learn”: it remembers.
That said, it is also intuitive that the lowest possible rank depends on the difficulty of the fine-tuning task with respect to the pre-training task. For example, when fine-tuning an LLM in a language that's different from the languages seen during pre-training, we should expect that we need a larger rank to achieve good performance. It would also be interesting to study how the lowest possible rank changes as a function of the depth of Transformer block. I’d expect lower ranks in the early layers (which have been shown to change little) and higher ranks in the later layers (which have been shown to change a lot).
LoRA has the potential to become a new paradigm shift in NLP, and we’re just beginning to see its full impact on the ML landscape in general. Watch this space.