Causal Modeling in Recommender Systems: A Primer
How causal graphs that approximate the real world help us solve the persistent problem of bias in ranking models
What made you open this article? I invite you to take 30 second to think about that.
I could think of a few reasons, such as “interest” (you were interested in the topic), “conformity” (you have a habit of reading things that land in your inbox/feed), “peer pressure” (your friend shared this with you), “credibility” (you found this piece linked in credible source), or “branding” (you have gotten value out of this Newsletter before), and so on. Welcome to the world of causal modeling.
Causal modeling is the idea of not only modeling an effect y given inputs x, but also taking into account the various reasons that cause x to result in y. This is not just a theoretical curiosity: Over recent years, causal modeling has emerged as an extremely effective tool to mitigate various biases in the ranking models underlying recommender systems.
At a high level, a causal model is a ranking model architecture the design of which is informed by a causal graph. A causal graph is a simplified representation of the real world, where the nodes correspond to entities and the edges correspond to directions of causation. In this causal view, we can then apply interventions such as removing an edge from the graph, also known as “backdoor adjustment”.
Before going any deeper, one thing should be made clear: the real world is a complex place, and any causal model is at best going to be a crude approximation of that complexity. Really, they’re first-order approximations: they help under some circumstances, but — just like a linear model approximating a sine curve — can get things entirely wrong in others.
With this disclaimer out of the way, let’s jump in and take a look at one of the very first causal models in Recommender Systems, Huawei’s 2019 PAL.
PAL (Guo et al 2019)
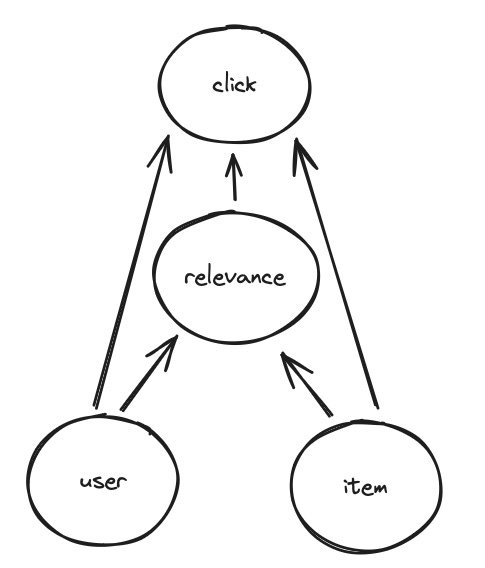
Huawei’s PAL tried to solve the problem of position bias: items that are shown first in the Huawei App Store are more likely to be clicked, making impressed rank a confounder for the property we actually want to learn, namely relevance. PAL’s causal graph has 5 nodes and 4 edges as follows:
PAL models this causal graph by introducing a second, shallow, MLP tower (an idea that has been widely adopted in the industry and which I’ve covered in depth here), which learns from positions alone. The output from this bias tower is then combined with the output from the main ranking model by multiplying their probabilities, although later versions of this two-tower design added the logits instead.

Importantly, at inference time we only use the prediction from the main tower, not the prediction from the bias tower. The reason is of course that we do not have the positions yet, we have yet to rank the items to get them. But even if the positions were somehow known in advance, we would not want to use them anyway because we want the model to be unbiased with respect to position at serving time. In causal modeling language, this is an example of a backdoor adjustment: we’ve removed the edge between position and click in the causal graph.
The authors build 2 different version of the DeepFM ranking model (which I wrote about here), one version with PAL and a baseline version with a naive way of treating item position: simply passing it as a feature into the model. Their online A/B test shows that PAL improves both click-through rates and conversion rates by around 25%, a huge lift, and one of the first demonstrations of the usefulness of causal modeling in recommender systems.
DICE (Zheng et al 2021)
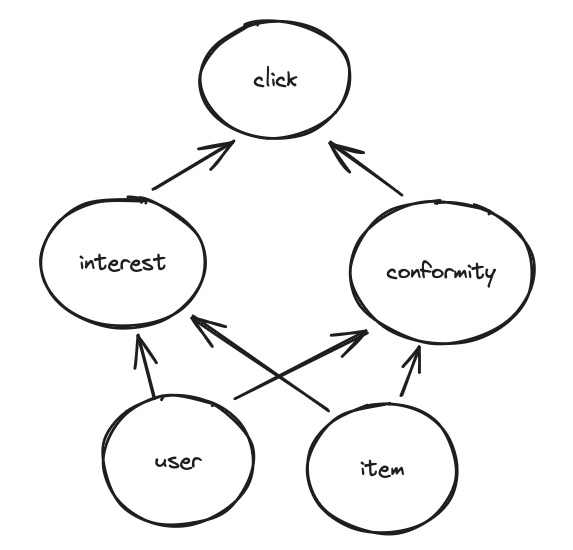
DICE (“Disentangling Interest and Conformity with Causal Embedding”) is one of the most-cited pieces of work on popularity bias in recommender systems. DICE assumes that clicks are caused by two phenomena, namely “interest” (the user is genuinely interest in the content) and “conformity” (the user would have clicked on anything). Consequently, the causal model in DICE consists of 5 nodes and 6 edges as follows:
DICE models this graph by learning two separate sets of user/item embeddings — one for conformity and for interest — using two different matrix factorization models that are trained in parallel. The key idea is to train these two models on different segments of the data, which the authors denote as O1 and O2:
in O1, positive examples (i.e. impressions with clicks) are more popular than negative examples,
in O2, positive examples are less popular than negative examples.
The authors argue that O2 is better suited for learning interest because the relatively unpopular positive training examples in this segment are particularly informative with respect to user interest. Meanwhile, O1 is better suited for learning conformity because all positive examples are also popular. Of course, this does not mean that all engagements in O1 are caused by conformity and all engagements in O2 are caused by interest. It’s an imperfect, yet empirically useful, partitioning scheme.
Using these two pairs of embeddings, the final prediction score is then computed as the sum
where the first term is the dot product of the user interest and item interest embeddings and the second term is the dot product of the user conformity and item conformity embeddings.
One additional architectural detail is the existence of an auxiliary loss to “encourage” the model to make these two sets of embeddings different from each other. Here, the authors choose the inverse of the L2 distance of the two embeddings, which is minimized if the two embeddings are far away from each other in the embedding space. The authors claim that this additional “discrepancy loss” helps with splitting the embeddings into interest and conformity, as shown in the plot below (although it would have been nice to see an ablation with the discrepancy loss turned off to see how much it really matters):
Compared to inverse propensity scoring (weighting training examples by inverse popularity), DICE achieves more than 2% improvement in NDGC on both the Movielens-10M and Netflix datasets, which the authors attribute to DICE’s superior modeling of popularity bias in the data using the dedicated interest and conformity embeddings.
MACR (Wei et al 2021)
MACR (“model-agnostic counterfactual reasoning”) is yet another way to look at recommendations from a causal point of view. The causal graph proposed in this work adds edges from user and item directly to the target, corresponding to user conformity (how likely is the user to click on anything) and item popularity (how likely is the item to be clicked on by anyone), resulting in 4 nodes connected via 5 edges as follows:
Under the hood, MACR models this causal graph with a 3-tower model, where the main tower models the relevance edge and the other two tower model the user and item edges, as follows:
The predictions from the ranking model is then combined with the outputs from these two additional towers as
where y is the prediction from the ranking model, y_I and y_U are the predictions from the user and item tower, respectively, and sigma is the sigmoid function converting the logits into click probabilities.
The intuition behind this solution is that we’d like to “force” the ranking model to learn to output larger logits y for a given training example if either the user is very unlikely to click overall or the item is very unlikely to be clicked on overall — in either case, an indicator of a particularly telling training example.
In contrast to DICE, the authors of MACR add an explicit backdoor adjustment at inference time, during which the prediction is computed as
i.e. we subtract the bias factor multiplied with a constant c. The idea behind this adjustment is to down-rank popular items during serving such as to counter-act popularity bias: if the item has a high probability of being clicked, we’re subtracting a large value. c is one of the hyperparameters in the MACR model (along with the weights for the user and bias loss terms), and the authors use grid search in the range from 20 to 40 to find its optimal value.
Lo and behold, MACR beats DICE on 5 different benchmark datasets, in some cases quite substantially, such as 17% NDCG on MovieLens-10M. Given the different training paradigms (interest/conformity embedding learning vs a 3-tower design) it is hard to pinpoint precisely what makes MACR better (assuming the results aren’t HARKed), but one aspect that certainly stands out in MACR is its explicit backdoor adjustment via the tunable c parameter, which may be a large contributor to its success.
TIDE (Zhao et al 2021)
Like DICE, TIDE (which I also covered here) assumes the presence of conformity in the causal graph explaining clicks. The key innovation in TIDE is to say that this conformity effect is time-dependent: user conformity tends to be strongest for fresh items where the ranking model has yet to learn the correct audience and hence the recommendations are still mostly random. In addition to conformity, different items also have different degrees of intrinsic quality, which is another effect modeled in TIDE but not in other causal models.
The resulting causal graph, with its 7 nodes and 8 edges, is the most complex we’ve seen in this survey:
Under the hood, the TIDE consists of a single matrix factorization model and a correction term that’s added to the model’s output predictions,
where
y is the result from a matrix factorization model for user u and item i,
y-hat is TIDE’s debiased prediction,
q_i is the quality term for item i,
c_i(t) is the time-dependent conformity term for item i.
For c, the authors choose weighted sum of the past interactions where the weights are exponentially decaying, i.e.
where
beta_i is a learnable parameter for each item,
t_l is the time of the item launch,
tau is a free “temperature” parameter that controls how rapidly conformity decays over time,
the sum is taken over all previous engagements of all users with the item.
This exponential decay is motivated by the empirical observation that item popularity does indeed appear to follow such a pattern for certain items:

At inference, the model prediction simplifies to
i.e. we zero out the conformity term (but not the quality term!) such as to debias the model, which is, as you probably know by now, a backdoor adjustment.
Ultimately, TIDE beats a host of competing algorithms, including DICE, on 3 different click prediction tasks. Again, these are different causal models and it is therefore hard to explain the success of TIDE, however the aspect that perhaps stands out the most is the time-dependence of the conformity effect, which intuitively makes a lot of sense and is probably a large contributor to TIDE’s success.
Coda
Causal modelers invent causal graphs that approximate reality and build models with an architecture that is informed by these graphs. Here, we’ve seen 4 examples:
PAL models clicks as the consequence of item positions and user/item relevance, which motivates the use of a two-tower model architecture, where the second tower learns from positions alone and is only used during offline training.
DICE models clicks as the consequence of interest and conformity, which motivates the use of two sets of user/item embeddings, one for interest and one for conformity, that are learned in parallel on distinct data partitions.
MACR models clicks as the consequence of relevance, item, and user, which motivates the use of a three-tower neural network.
TIDE models clicks as the consequence of relevance, item quality, and user conformity, where item quality is static but user conformity decays exponentially with time. At training time, both the quality and conformity terms are added to the model prediction, but at serving time only the quality term.
Which one of these is the best one? It depends. Causal modeling is by no means a solved problem, and we are still learning what works and what does not. From personal experience, I’ve seen some of the approaches discussed here work in some problems but not in others. Again, causal models make first-order corrections, which can be useful in some cases but not in others. The unfortunate reality is that we don’t have (yet) a good theory to guide us. The only way to find out if a particular causal model works for your problem is to try it.